작성: 숲사람
Red-Black Tree 란?
RB-Tree 는 Radix-Tree와 더불어 Linux Kernel에서 가장 많이 사용하는 Tree 자료구조이다. I/O scheduler(CFQ, deadline 등), ext filesystem, Virtual memory areas 등 Kernel의 여러 Subsystem에서 사용된다. 기존 Tree자료구조의 단점은 최악의 경우 노드가 Linked-List의 형태로 저장되어 탐색 시간복잡도가 O(N) 이 된다는 점이다. 하지만 RB Tree는 노드의 삽입과 삭제가 이루어 질때, Tree가 자동으로 회전하며 O(logN)의 시간복잡도를 보장한다.
이 글에서는 일반적인 RB Tree에서 가장 복잡한 연산인 삽입과 삭제가 어떤 방식으로 동작 하는지 알아본다. 경우의 수만 잘 따지고 그때그때 어떻게 해주는지 규칙만 잘 파악하면 쉽게 따라갈 수 있다. 이를 기반으로 해서 다음 글에서 Linux Kernel 에서 RB Tree가 어떻게 구현되었는지 살펴 볼것이다.
RB tree의 5가지 규칙
노드의 삽입과 삭제연산을 할때마다, 아래의 규칙을 만족시키도록 트리의 노드위치를 변경하거나 유지하는것이 RB Tree이다.
- 노드는 빨간색 검은색 둘 중 하나다(A node is either red or black)
- Root 노드는 검은색이다. (The root is black)
- 모든 말단 노드는 검은색이다 (All leaves (NULL) are black)
- 빨간색 노드는 중첩될 수 없다. (Both children of every red node are black)
- 각 말단노드의 Black Height는 모두 동일하다 (Every simple path from root to leaves contains the same number of black nodes)
Black Height: 말단노드에서부터 Root노드 사이의 검은색 노드 갯수
삽입 연산
새노드가 트리에 삽입될때, 부모노드는 검은색인경우 빨간색인 경우 두가지가 있다. 아래 설명된 각각의 경우의 수에따라 5가지 종류의 삽입연산이 필요하다.
새노드 삽입 insert_case1() 수행
-검은색에 삽입 -> 문제가 되지 않음
-빨간색에 삽입
(1) 삼촌도 빨간색인 경우 insert_case3(n)
부모,삼촌 검은 색, 할아버지 빨간색으로
(2) 삼촌이 검은색인 경우 (여기서 삼촌은 할아버지의 오른쪽 자식으로 가정)
1) 삽입노드가 부모노드의 오른쪽 자식인 경우 insert_case4(n)
삽입노드와 부모노드를 회전시켜 부모노드를 삽입노드의
왼쪽 자식으로 만든다. --> 2)과 구조가 됨
2) 삽입노드가 부모노드의 왼쪽 자식인 경우 insert_case5(n)
부모노드를 검은색 할아버지 노드를 빨간색으로 바꾸고
오른쪽회전 (부모노드가 루트위치로)
일부 삽입연산은 트리의 회전연산이 필요하다(rotation_left() 및 rotation_right()). 회전연산은 매개변수로 전달된 노드의 자식을 치켜세워주는 연산이라고 생각하면 이해하기 쉽다 : 자식이 위로 부모는 아래로. 아래 그림은 부모노드(O)와 자식노드(N) 기준으로 rotation_left 회전이 일어날때 트리의 구조 변화이다.
P P
/ /
(O) (N)
/ \ / \
l (N) --> (O) r
/ \ / \
m r l m
각각의 삽입 연산 동작 방식은 아래와 같다.
insert_case1(n)
{
if (부모노드가 없는경우) -> n을 블랙 (루트노드가됨)
else (부모노드 있으면)
insert_case2(n) 수행
}
insert_case2(n)
{
if ( 부모노드가 블랙인경우 )
그냥 삽입해도 문제 안되므로 return
else(부모노드 빨강)
insert_case3(n) 수행
}
insert_case3(n)
{
if( 삼촌노드 빨간색이면 && 삼촌노드 있으면)
부모,삼촌노드 검은색으로
할아버지노드 빨간색으로
insert_case1( 할아버지노드) " 재귀적으로 수행 !!"
else "그외 나머지 경우 (삼촌 노드가 검정색 || 삼촌노드 없으면)"
insert_case4 (n)
}
insert_case4()는 case5 함수를 수행할 구조로 만드는 작업이다.
insert_case4(n)
{
if (부모노드가 할아버지 노드의 왼쪽자식 && 새노드가 부모노드의 오른쪽자식 )
rotation_left(부모노드)
n = n->왼쪽노드
if(부모가 할아버지의 오른쪽 자식 && 새노드가 부모 노드의 왼쪽 자식)
rotation_right(부모노드);
n = n->오른쪽노드
둘다 아니거나 위내용을 수행했으면
insert_case5(n) 수행
}
insert_case5(n)
{
부모는 검은색으로 할아버지는 빨간색으로
if ( 부모가 할아버지의 왼쪽자식 && n이 부모의 왼쪽자식 )
rotation_right( 할아버지 노드)
else (부모가 할아버지 오른쪽 자식 && n이 부모의 오른쪽 자식 )
rotation_left( 할아버지 노드)
}
삭제 연산
삭제 연산은 삽입 연산보다는 다소 복잡한데, 삭제되는 노드를 처리해야하고, 삭제된 자리를 새로운 후계자 노드로 변경해야하기 때문이다.
삭제되는 노드 처리
삭제되는 노드에 대체되는 노드를 복사한다. 색은 삭제되는 노드색을 유지하고, 노드만 바로 복사된다. 대체될 수 있는 후계자는 이진트리 삭제와 마찬가지로 left 하위트리 에서 가장 큰 노드인데(삭제 노드의 왼쪽sub트리는 Inorder Predecessor 오른쪽은 Inorder successor라고 표현함), 보통 맨 아래 노드이고 (leaf node가 1개와 Null leaf1개) 이거나 (Null leaf만 두개)인 경우밖에 없다. 중요한건 이 대체되는 후계 노드가 그 자리에서 삭제 된다는것인데, 이때 RB트리의 규칙이 무너지는 경우가 있기 때문에, 대체되는 노드를 기준으로 아래 2번의 알고리즘을 따르게 된다. 가령 아래 트리에서 노드 40이 삭제된다면 그자리를 대체할 수 있는 후계노드는 노드 30이 될것이다.
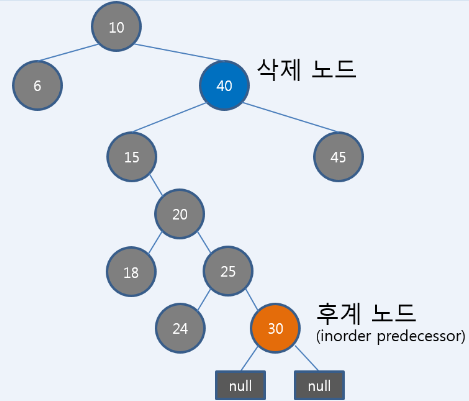
아래 설명에서 n은 대체될 노드의 자식이다. 일반 노드가 될 수 도 있고 Null leaf(검은색)가 될수도 있다. 즉, 트리에서 삭제되는 노드 기준으로 트리 balancing동작을 시키는 것이 아니라 후계자 노드 기준으로 balancing동작 수행한다.
후계자 노드 처리
후계 노드가 삭제되는 것으로 판단하면 된다. 후계 노드가 빨간색일 경우와 검은색일 경우에 따른 케이스로 구분하면 된다. 아래 형제,부모,조카는 대체될 후계 노드 기준으로 위치한 노드이다. 실제로는 대체될 후계노드의 자식노드기준으로 볼 수도 있는데. 그이유는 대체될 노드는 삭제노드 위치로 변경되고 대체될 노드의 자리에는 어차피 그 노드의 자식노드가 위치할 것이기 때문이다.
- 후계노드가 빨간색 -> 문제 없음
- 후계노드가 검은색
- 형제가 빨간색인 경우 delete_case2(n)
- 형제가 검은색인 경우
(3) 부모노드 검은색, 형제의 양쪽 자식이 모두 검은색 : delete_case3(n)
->형제노드만 빨간색으로
(4) 부모노드는 빨간색, 형제의 양쪽 자식이 모두 검은색 : delete_case4(n)
->형제:빨간색 부모:검정색
(5) 삭제노드와 가까운 조카노드가 빨간색일때 : delete_case5(n)
-> 형제와 조카노드 색교환, 형제기준 조카노드를 올리는 방향의 회전
(아래 case6 조건으로 변경됨)
(6) 삭제노드와 먼 조카노드가 빨간색 (가까운조카색 관계없음) : delete_case6(n)
형제는 부모노드 색으로, 부모는 검은색으로
멀리있는 조카노드 검은색으로
부모노드 기준 형제를 올리는 방향의 회전
삭제되는 후계자 노드 위치 기준으로 delete_one_child() 부터 시작한다.
"여기서 n은 실제 트리에서 제거될 후계 노드의 자리를 차지하게 될 노드임에 주의"
delete_one_child(n)
{
child = is_leaf() "n의 자식"
child(n의 자식)를 삭제될 n(후계노드)있던 자리로 변경
if( n == 블랙)
if ( child == 레드)
child 블랙으로 변경
else
delete_case1(child) 호출
"n의 자식으로 case 1 부터 start!"
"여기서 child의 위치는 후계노드의 원래 위치와 동일함"
}
"여기서 n은 대체노드의 자식노드 child임에 주의"
delete_case1(n)
{
if (삭제노드의 부모가 NULL이 아니면)
delete_case2(n) 호출
}
"형제를 검은색, 부모를 빨간색으로 바꾸고 left/right회전!"
delete_case2(n)
{
if (형제 == 레드)
부모노드를 빨간색, 형제노드를 검은색 변경
if ( n == 부모의 왼쪽자식)
rotation_left(부모노드)
else
rotation_right(부모노드)
delete_case3(n) 호출
}
delete_case3(n)
{
if (형제==블랙 && 부모==블랙 && 형제 좌/우 자식==블랙)
형제를 빨간색
deletion_case1(부모노드) 호출
else
deletion_case4(n) 호출
}
delete_case4(n)
{
if (형제==블랙 && 부모==레드 && 형제 좌/우 자식==블랙)
형제를 빨간색
부모를 검정색으로
else
deletion_case5(n) 호출
}
delete_case5(n) //case6 를 수행할 구조로 만드는 작업
{
if (형제 == 블랙)
if (n이 부모노드의 왼쪽자식 && 형제 오른쪽자식==검정 && 형제 왼쪽자식==빨강)
형제노드 빨간색으로
형제 왼쪽 자식 검은색으로
rotation_right(형제노드)
else if (n이 부모노드의 오른쪽 자식 && 형제 왼쪽자식==검정 && 형제 오른쪽자식==빨강)
형제노드 빨간색으로
형제 오른쪽 자식 검은색으로
rotation_left(형제노드)
deletion_case6(n) 호출
}
delete_case6(n)
{
형제색 = 부모의 색으로
부모색 = 검정색으로
if (n이 부모의 왼쪽 자식이면)
형제의 오른쪽자식 검정색 으로
rotation_left(부모노드)
else "n이 부모의 오른쪽 자식"
형제의 왼쪽자식 검정색 으로
rotation_right(부모노드)
}