2.2. Computing Parameters Analytically

• 2.2.1. Normal Equation
• 2.2.2. Normal Equation Noninvertibility

2.2.1. Normal Equation

Normal Equation은 최적의 $\theta$ 를 구할 수 있는 또다른 방법이다. gradient descent 와는 다른 방식으로 각각 장/단점이 있다. Normal Equation은 $\theta$ 를 반복계산 없이 공식하나로 한번에 구할 수 있다. 다음의 training set을 보자.

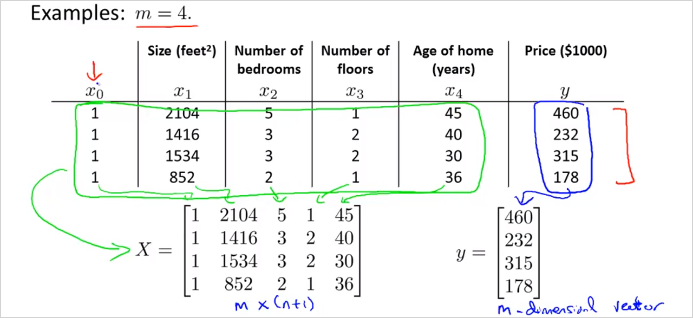
4개의 feature가 있고 결과가 있다. 이것을 각각 X matrix와 y 벡터로 복사한다. 계산의 편의를 위해 1을 갖는 $x_0$ 열이 추가되었음에 유의. 이것을가지도 아래 Normal Equation 공식에 대입해 계산하면 바로 $\theta$를 구할 수 있다!

$\theta = (X^TX)^{-1}X^Ty$

이렇게 계산된 $\theta$ 는 cost function J를 최소화하는 값이다.

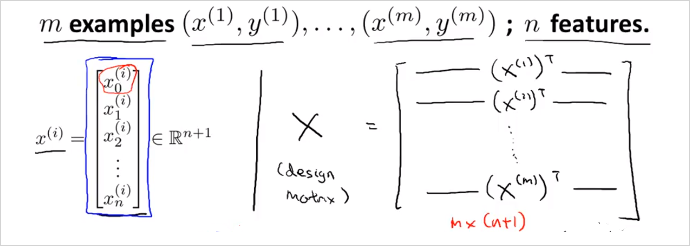
만약 $i$번째 하나의 training data가 위의 $x^{(i)}$ 처럼 n + 1 크기의 벡터로 주어진다면, 이것으로 우측과 같이 Design Matrix X를 만든다. (결국 이전 예시처럼 테이블을 그대로 matrix에 복사한것과 동일한 구성임)

더 간단한 예를들면 아래와 같다.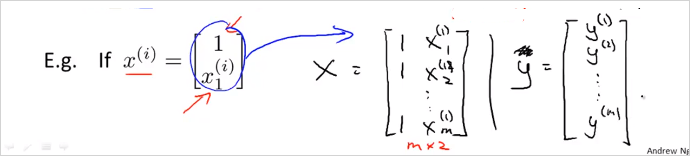

$\theta$ 를 구하는 Octave 명령어

pinv(X'*X)*X'*y

반복 계산도 필요없고 적절한 $\alpha$를 찾아야하는 수고가 없다. 또한 Feature scaling도 필요없다. 이렇게 좋은 방법이 있다니? 그러나 결론적으로Normal Equation에 매우 치명적인 단점이 있다. n(feature갯수)가 엄청 커지면 Normal Equation은 못쓴다. 복잡도가 $O(n^3)$ 으로 연산속도가 엄청나게 느려지기 때문이다.

Gradient descent 와 Normal equation을 비교하면 아래와 같다.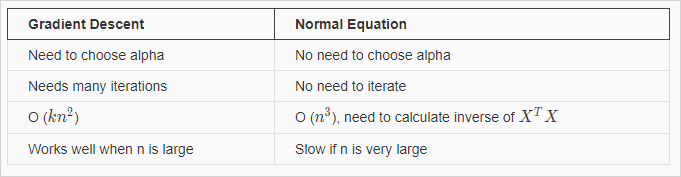

보통 n=10000 정도까지는 Normal equations을 사용해도 괜찮다고 한다. 현대 컴퓨팅 파워로 이정도계산 까지는 실용적인 속도를 얻을 수 있다.

2.2.2. Normal Equation Noninvertibility

역행렬이 없는 Normal Equation은 어떻게 구해야할까?
$\theta = (X^TX)^{-1}X^Ty$
$X^TX$ 가 역행렬이 없는 경우가 있기 때문이다.

다음의 두가지 경우에 $X^TX$ 에 역행렬이 없다.

1번은 각 feature가 $x_1 = (3.28)^2x_2$ 처럼 선형적으로 종속적인 관계일때이다. 이럴땐 둘 중 한feature를 제거해도 된다.
두번째는 피쳐갯수(n)이 training set갯수(m)보다 많을때이다. 이럴땐 어떤 feature들을 지우거나, regularization기법을 사용한다.