5. Neural Networks: Learning

• 5.1 Cost function
• 5.2. Backpropagation Algorithm
• 5.3. Backpropagation Intuition
• 5.4. Backpropagation in Practice

5.1 Cost function

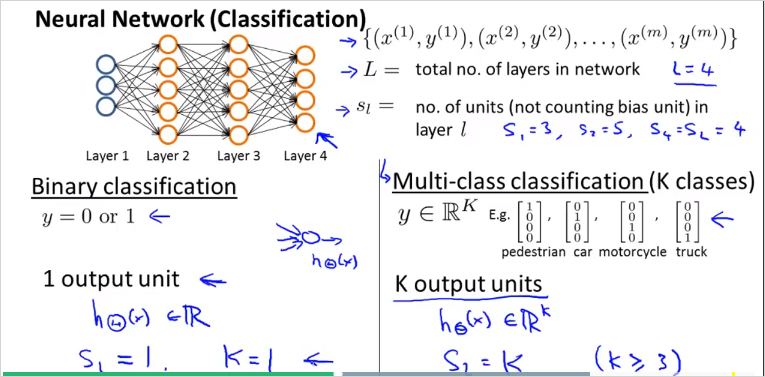
두종류의 classification 에대해서 알아볼것이다. 하나는 이진 분류, 나머지하나는 멀티 분류이다. 최종 분류되는 종류 Class갯수는 $K$로 나타낸다. 따라서 $h_\theta(x)$ 는 $K$ 차원 벡터다. 중요한점: 예측 값 y 벡터는 class갯수 K의 크기를 갖는 벡터다. $K \times 1$ 의 크기를 갖는다. 한 벡터는 위 그림처럼 최종 분류된 하나의 class만 1이고 나머지는 0으로 구성된다.

• 용어 정리.
  $L$ = total number of layers in the network
  $s_l$ = number of units (not counting bias unit) in layer l
  $K$ = number of output units/classes

Logistic regression의 경우, cost function은 다음과 같이 정의 했었다.

$J(\theta) = -\frac{1}{m} \sum_{i=1}^{m} \left[ y^{(i)} \log h_\theta ( x^{(i)} ) + \left( 1-y^{(i)} \right) \log \left( 1-h_\theta ( x^{(i)}) \right) \right] + \frac{\lambda}{2m} \sum_{j=1}^{n} \theta_{j}^{2}$

Neural Network에서는 다음과같이 정의한다.

$h_\theta(x) \in \mathbb{R}^k, \quad \left( h_\theta (x) \right)_i = i^{\mathrm{th}} \text{ output}$

윗첨자 $i$는 $i$ 번째 output을 의미한다($i \leq m$). $(h_\theta(x))_i$의 $i$는 $h_\theta(x)$ 의 $i$번째 element 를 의미 ($i \leq m$)
$h_\theta(x)$ 는 $K$ 차원 벡터

$J(\theta) = -\frac{1}{m} \left[ \sum_{i=1}^{m} {\color{royalblue}{\sum_{k=1}^{K}}} y_{\color{royalblue}{k}}^{(i)} \log { {\left( h_\theta ( x^{(i)} ) \right)}_{\color{royalblue}{k}} } + \left( 1-y_{\color{royalblue}{k}}^{(i)} \right) \log \left( 1-h_\theta ( x^{(i)}) \right)_{\color{royalblue}{k}} \right] + \frac{\lambda}{2m} {\color{royalblue}{\sum_{l=1}^{L-1} \sum_{i=1}^{s_L}}} \sum_{j=1}^{s_{L+1}} \color{royalblue}{(\Theta_{ji}^{(l)})^2}$

${\color{royalblue}{\sum_{k=1}^{K}}}$ : 는 class가 K 개 이므로 K개의 output을 모두 더함을 의미한다. 그래서 각 항에 아랫첨자 $k$가 존재한다. $y_k$ 는 각 가설함수에 상응하는 k번째 실제값이다.

${\color{royalblue}{\sum_{l=1}^{L} \sum_{i}^{}}} \sum_{j=1}^{n} \color{royalblue}{(\Theta_{ji}^{(l)})^2}$ : 항은 Regularization 용이며, 모든 $\Theta$ 요소를 다 더한다는 의미이다. $\Theta$가 각 레이어 마다 $s_{L+1} \times (s_L + 1)$ 크기 만큼 있기 때문이다.
참고로 여기서 $j$ 는 계산될 layer 유닛 번호, $i$는 현재 layer 유닛 번호이다.

• Initial parameter $\Theta$
  우리는 시작할때 완전히 랜덤값의 weight $\Theta$를 가지고 시작할것이다. gradient descent 가 반복될때마다. 올바른 $Theta$ 값이 선택될(학습될)것이다. 그런데 먼저 gradient를 계산해야한다. 그때 필요한것이 Backpropagation Algorithm 알고리즘이다.

5.2. Backpropagation Algorithm

머신러닝은 cost function J()에 대한 미분을 계산해야한다. Backpropagation는 이 미분을 효율적으로 계산하는 방법이다. 늘 그랫듯이, parameter $\theta$를 학습하기 위해, cost function J()를 최소화해야 하는데 Backpropagation 이 그것을 위한 방법이다. Input layer에서 출발해서 output을 구하는 forward propagation과는 반대로, BP는 output layer에서 시작한다. 즉, 마지막 결과의 'error'를 먼저 구하고, 해당 error 값을 이용해 각각의 node에서의 error 를 계산한다.(https://wikidocs.net/4262)

결국 계산해야할 값은 cost function J()와 J()의 미분도함수(gradient)이다. 이전에 보았듯이 Forword propagation은 아래와 같이 계산된다.

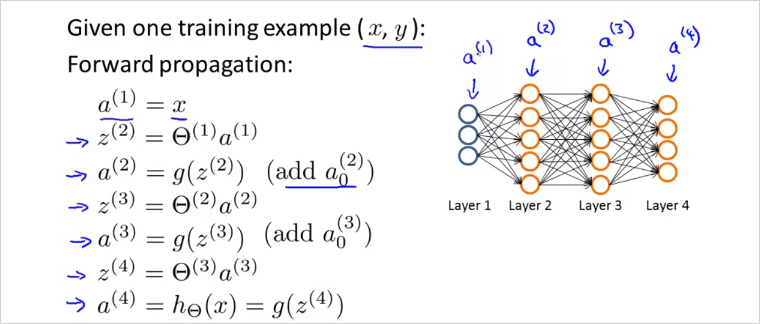
BP의 에러값 $\delta$는 다음의 그림을 보면 직관적이다. 최종 결과물의 오차는 단순하다. (output - expected) 이다. 이 오차는 누적된것일 것이고, 그 오차들을 이전레이어부터 추적하는것이다. 그렇게 오차를 최소화 하는 방향으로 $\Theta$ 를 구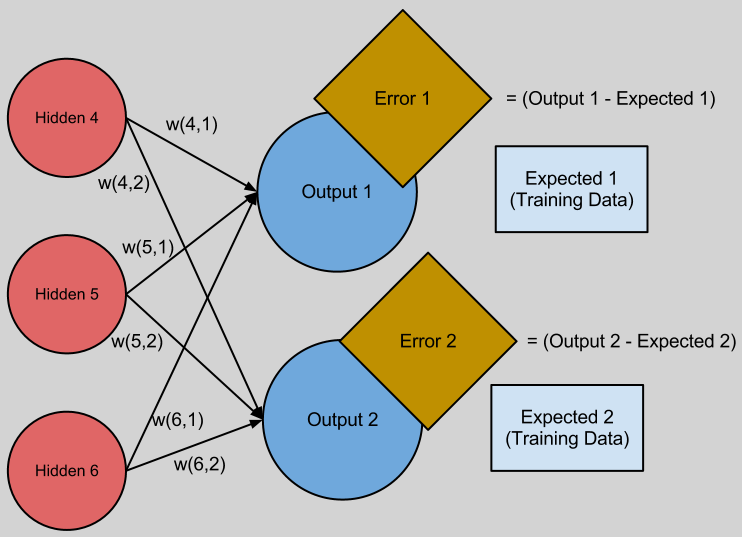할 수 있을것.

(출처 : http://andrew.gibiansky.com/blog/machine-learning/machine-learning-neural-networks/)

만약 $w(6,2)$이 매우 크다면, 매우 큰 output2 가 만들어질 것이고 이것은 매우 큰 Error2를 만든다. 이것은 BP를 할때 큰 비중이 할당될 것이다.

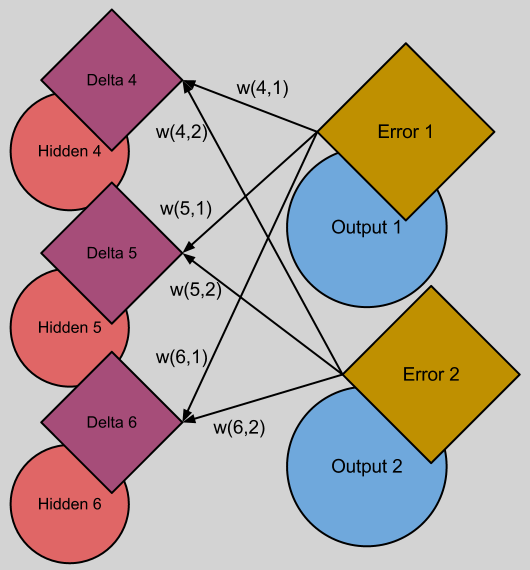
어쨋든 BP를 마치면 모든 유닛에 $\delta$를 구했다면 cost fuction J()의 Gradient(미분도함수)가 나온다.

Back propagation은 다음과 같이 계산한다. $\delta$ 는 l 레이어에 있는 node j 에 오류가 있는지를 의미한다.
Layer가 4개인 경우, $\delta^{(4)}$ 는 단순하게 a(4) 에서 label y 를 뺀값이나, 다음 $\delta^{(3)}$ 부터는 가중치($\Theta$)를 고려해서 계산된다. $\delta^{(l)} = ((\Theta^{(l)})^{T} \delta^{(l+1)}) .* g'(z^{(l)})$
$g'(z^{(3)})$ 은 미분도함수로 $g'(z^{(l)}) = a^{(l)}.*(1 - a^{(l)})$ 과 같이 계산된다. $\delta^{(1)}$ 는 계산하지 않는다.'

최종적으로 위의 계산을 마치면, 만약 $\lambda = 0$ 일때, 아래와 같은 결과가 나옴을 증명할 수 있다(고 한다).

$\dfrac{\partial }{\partial \Theta_{i,j}^{(l)}}J(\Theta) = a_j^{(l)}\delta_i^{(l+1)}$

이것을 계산하는 BP 알고리즘은 아래와 같다. 이것은결국 cost function J()의 미분도함수를 계산 하는 과정이다.

$\Delta$ 는 $a_j^{(l)}\delta_i^{(l+1)}$ 를 누적해서 더한것을 의미한다. (그래서 0으로 초기화해서 시작) 순서대로 살펴보면 먼저 Forward propagation 을 하여 $a^{(l)}$ 계산을 마친다. 그 뒤에 back propagation으로 각 $\delta$ 를 구한다. 그리고 그 두항을 곱해서 $\Delta$에 누적해서 더한다. (j = 0) 이 아닐때는 regularization \lambda 항이 추가됨에 유의 j = 0일때는 bias 항이기 때문에 필요없음. 그렇게 해서 나온 결과를 $D_{ij}^{(l)}$ 라고 표현할 것이다. $D_{ij}^{(l)}$ 가 결국 cost function J() 의 미분도함수가 되는것이다.

$D_{i,j}^{(l)} = \dfrac{\partial J(\Theta)}{\partial \Theta_{i,j}^{(l)}}$

BP 이해 추천 사이트:
https://www.youtube.com/watch?v=Ilg3gGewQ5U
http://neuralnetworksanddeeplearning.com/
http://neuralnetworksanddeeplearning.com/chap2.html

5.3. Backpropagation Intuition

Backpropagation 의 의미를 좀 더 이해해보자. 먼저 FP의 경우 $z_1^{(3)}$은 아래와 같이 가중치를 곱한 형태로 계산됨을 이미 살펴보았다. BP또한 방향만 반대 일뿐 매우 유사하다. $\delta$ 를 방향만 반대로 계산 하는것이다.

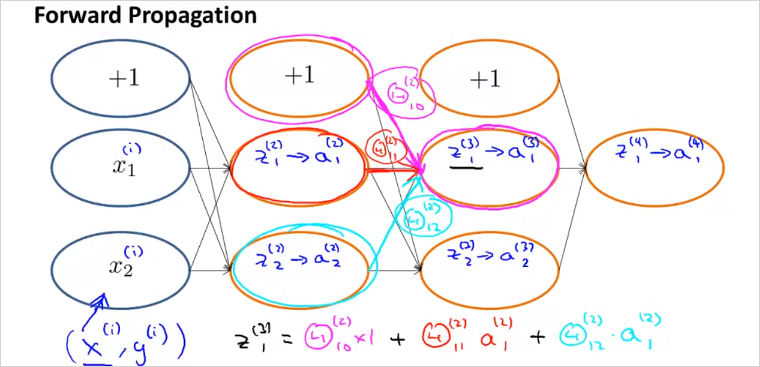
BP는 아래와 같이 반대로 계산된다. $\delta_2^{(2)}$는 layer 3을 향하는 가중치($\Theta$)를 곱해서 계산된다. $\delta_2^{(3)}$ 도 마찬가지다. bias unit은 계산되지 않음에 유의

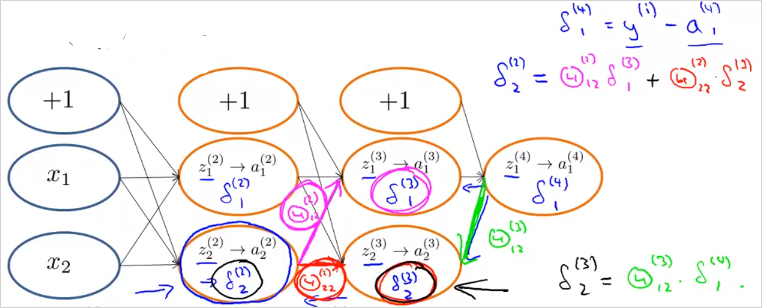
5.4. Backpropagation in Practice

Octave에서 실제로 어떻게 사용하는지 알아보자.

5.4.1. A. Implementation Note: Unrolling Parameters

결국 NN 에서는 아래의 matrix를 이용하게 된다. $\theta$는 weitght, $D$ 는 cost function J()의 미분 도계수를 의미한다.
$\begin{align*} \Theta^{(1)}, \Theta^{(2)}, \Theta^{(3)}, \dots \newline D^{(1)}, D^{(2)}, D^{(3)}, \dots \end{align*}$

fminunc() 등을 사용해 optimizing 하기 위해서 아래와 같이 각 matrix를 하나의 벡터로 합친다(unroll)

thetaVector = [ Theta1(:); Theta2(:); Theta3(:); ]  
deltaVector = [ D1(:); D2(:); D3(:) ]

각 matrix는 아래와 같은 명령으로 다시 분리할 수 있다.

Theta1 = reshape(thetaVector(1:110),10,11)  
Theta2 = reshape(thetaVector(111:220),10,11)  
Theta3 = reshape(thetaVector(221:231),1,11)

예를들어 3개의 레이어가 있고 각 unit의 갯수가 다음과 같다고 할때 아래와 같이 나타낼 수 있다.

결국 이전 챕터에서 살펴 보았던 BP알고리즘을 더욱 간단히 도식화 하면 다음과 같다. fminunc() 의 parameter인 @costFunction이 cost J($\Theta$)와 그의 미분계수 $D$를 구하는 함수다.

5.4.2. Gradient Checking

BP에 문제가 없는지 확인할 수있는 방법이다. 항상 사용됨.

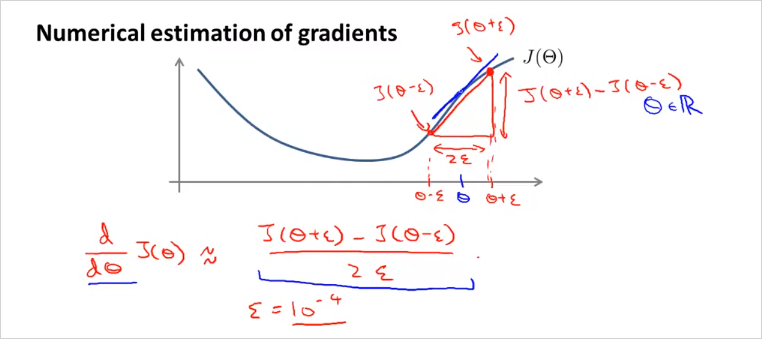
$\Theta$가 하나일때 2$\epsilon$ 만큼 떨어진 두 지점의 기울기를 이용하면 J() 의 미분계수를 추정할 수 있을것이다. 그리고 Octave에서 다음과 같이 implement 된다.

gradAppros = (J(theta + EPSILON) - J(theta - EPSILON)) / (2*EPSILON)

멀티 parameter인 경우로 보다 일반화하면 다음과 같다.

그리고 Octave에서 다음과 같이 implement 된다.

epsilon = 1e-4;  
for i = 1:n,  
  thetaPlus = theta;  
  thetaPlus(i) += epsilon;  
  thetaMinus = theta;  
  thetaMinus(i) -= epsilon;  
  gradApprox(i) = (J(thetaPlus) - J(thetaMinus))/(2*epsilon)  
end;

그리고 Gradient Checking으로 계산된 gradApprox(i)과 BP로 계산된 미분계수 $D$벡터가 같은지 확인하면 되는것이다. gradApprox(i) = DVec 따라서 Gradient Checking을 사용하는 방법을 정리하면 다음과 같다.

다시 Training하기 전에 Gradient Checking을 끄지 않으면 엄청 느려질 수 있음에 주의해야한다. Once you have verified once that your backpropagation algorithm is correct, you don`t need to compute gradApprox again. The code to compute gradApprox can be very slow.

5.4.3. Random Initialization

기존처럼 $\Theta$ 의 초기값을 0으로 정하는것은 NN에서 동작하지 않는다. 그이유는 잘 이해하지 못했음. 따라서 다음과 같이 $\Theta$의 초기값을 구한다. 결과적으로 $\Theta$ 의 범위는 $-\epsilon$ ~ $\epsilon$ 이 될 것이다.

Octave로 implement 하면:

If the dimensions of Theta1 is 10x11, Theta2 is 10x11 and Theta3 is 1x11.  

Theta1 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON;  
Theta2 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON;  
Theta3 = rand(1,11) * (2 * INIT_EPSILON) - INIT_EPSILON;

rand(x,y) is just a function in octave that will initialize a matrix of random real numbers between 0 and 1.

5.4.4. Putting it Together

지금까지 NN에서 다룬 내용을 모두 종합해보자.

첫번째로 적절한 Network architecture를 선택한다. 그것은 다음을 선택하는것이다.

• Input Unit 갯수
• Output Unit 갯수
• layer 당 hidden unit 갯수 (많을수록 성능 향상, 연산 cost 증가)

Training a Neural Network

1. Randomly initialize the weights
2. Implement forward propagation to get $h_\Theta(x^{(i)})$
3. Implement the cost function
4. Implement backpropagation to compute partial derivatives

4번까지 정리하면 이런 모양

1. Use gradient checking to confirm that your backpropagation works. Then disable gradient checking.
2. Use gradient descent or a built-in optimization function to minimize the cost function with the weights in theta.

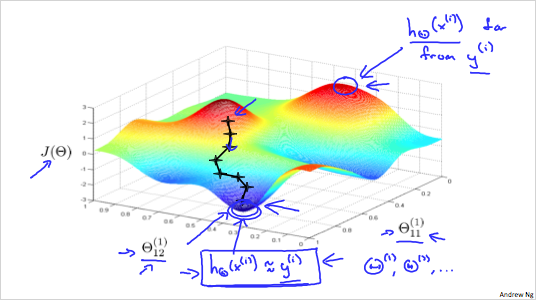
최고점은 $h_\theta(x)^{(i)}$ 가 실제 값 $y^{(i)}$ 와 가장 차이가 큰 것이고, 최저점은 $h_\theta(x)^{(i)}$ 가 실제 값 $y^{(i)}$ 에 가장 가깝다는 뜻이다. gradient descent는 기울기를 하강하는 것이고, BP는 기울기를 하강할때 방향을 설정하는것과 같다.